Tag: Independent Sites

The concepts of stoichiometric and site binding constants

Eva Muñoz

Download: The concepts of stoichiometric and site binding constants

The interaction between a monovalent ligand L and a multivalent receptor R involves the presence of various species, including the complex of R fully saturated with a number of ligands, and intermediate complexes of R partially saturated. This scenario can be described in terms of reaction schemes following two approaches:

 

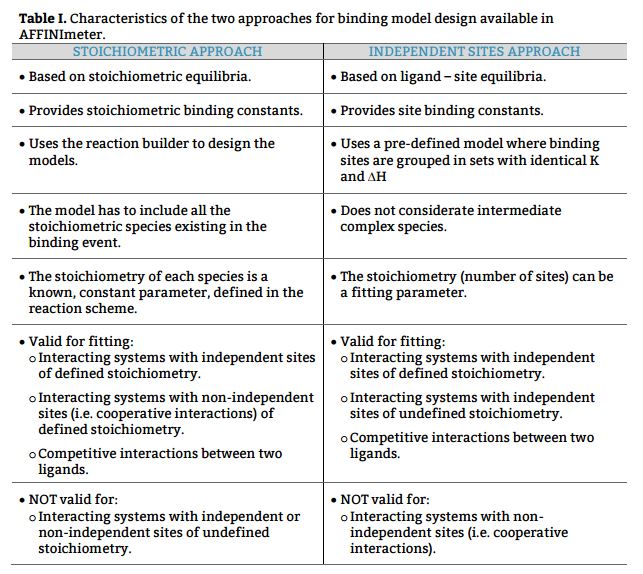
  1. Based on equilibria between existing stoichiometric species (Stoichiometric approach).
  2. Based on equilibria between L and specific interaction sites of R (independent sites approach).
For a better understanding, let´s consider a particular case where L binds to a bivalent receptor:

1. Stoichiometric approach

This approach uses reaction schemes based on equilibria between stoichiometric species and yields stoichiometric binding constants. A model based on stoichiometric equilibria is valid to fit data of both independent and non-independent events and therefore, it is of wider applicability.

Here, the reaction scheme includes a first equilibrium between the free species and the intermediate RL and the second equilibrium between RL + L and RL2 (Fig. 1). The corresponding binding constants, K1 and K2, are denominated stoichiometric binding constants since they refer to equilibria between stoichiometric species.

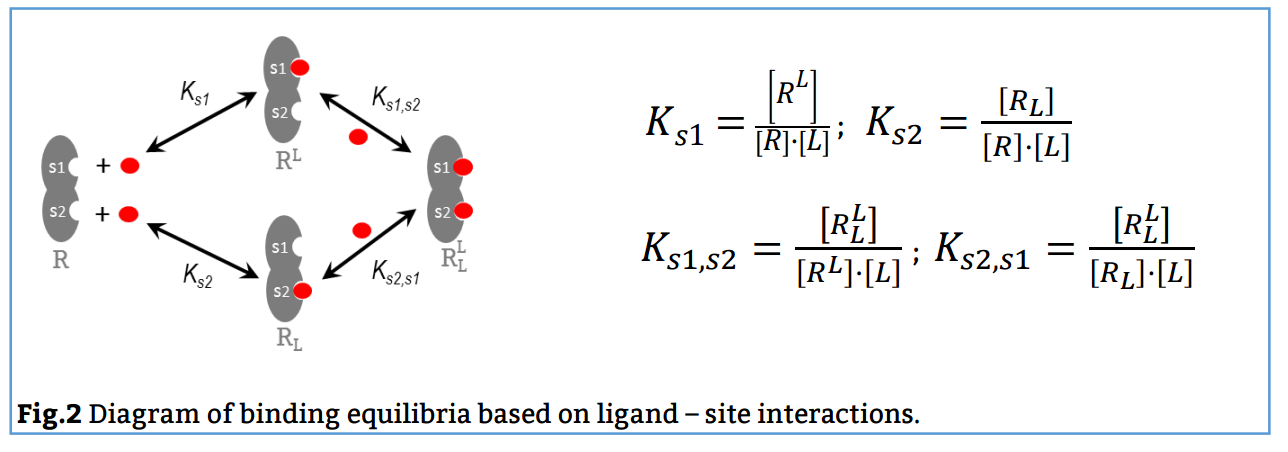
2. Independent site approach

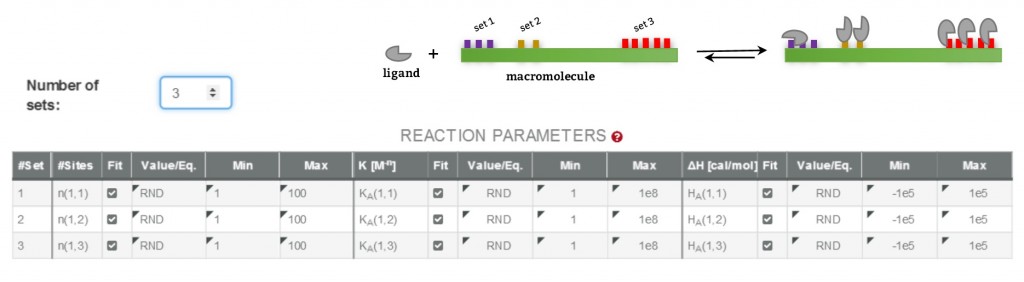
This approach uses a reaction scheme based on the binding of the ligand to individual sites present in the receptor and considering that all the sites are independent; thus, it supplies site binding constants.

In this case, the reaction scheme considers the presence of two sites in the bivalent receptor and two intermediate complexes (R, L and RL) formed when the ligand binds to s1 or s2 and consequently, the existence of a total of 4 equilibria (Fig. 2). The corresponding binding constants, Ks1, Ks2, Ks1, s2 and Ks2, s1, are denominated site binding constants since they refer to equilibria between L each specific site of R.

If you want to know more about how to get the stoichiometry (number of sites) and site binding constants with the independent sites approach you can click on the following button:
 

 

The course of Isothermal Titration Calorimetry data analysis: second part

AFFINImeter

In the second part of this course, we are going to show you how to perform the analysis of binding isotherms considering an independent sites approach.
This approach uses a reaction scheme based on the binding of the ligand to individual sites present in the receptor and considering that all the sites are independent; thus, it supplies site binding constants.
This approach offers a sole reaction scheme where a receptor with a certain number of sites “n” binds to the ligand.
The sites are grouped into sets to discern between sites that are non-equivalent.

If you want to know more about how to get the stoichiometry (number of sites) and site binding constants with the independent sites approach you can click here:

Stoichiometric and site constants – two approaches to analyze data with AFFINImeter

The first video tutorial presented is about how to use an independent sites approach to perform fittings:

——————————————————————–

Into another subject, to introduce the second fitting approach that can be performed with AFFINImeter (Stoichiometric equilibria), we will describe how to use the model builder.
This original tool allows to design and apply your own binding model in an easy way. Check the following video to know the versatility of the model builder:

Finally, if you want to try the Model Builder click here:

Model Builder

 

Stoichiometric and site constants: two approaches to analyze data with AFFINImeter.

AFFINImeter

The interaction between two species, i.e. a protein and its ligand, is defined by means of the equilibria existing between free and bound species and the binding constant(s) associated to each equilibrium. This scenario can be described in terms or reaction schemes following two approaches:

a) Based on equilibria between existing stoichiometric species, to obtain stoichiometric binding constants and

b) Based on equilibria between the ligand and specific interaction site(s) of the protein, to obtain site binding constants.

affinimeter-approaches-small

The understanding of both approaches/type of binding constants is key for a correct interpretation of the results after data analysis, in order to get key structural and mechanistic information of the binding event; i.e. the presence or absence of cooperative interactions when a ligand binds to a multivalent receptor.
The design of binding models for ITC curve fitting with AFFINImeter can be done following these two approaches, to perform analysis based on stoichiometric and/or site binding constants.

The scientific team of AFFINImeter has just released three NOTES regarding this subject to guide users into the right selection of binding model approach and a better understanding of stoichiometric vs site binding constants.

Comparative table of the two approaches for binding model design available in AFFINImeter
Characteristics of the two approaches for binding model design available in AFFINImeter

 

DOWNLOAD PDF FILES HERE:

Or visit the RESOURCES section of AFFINImeter web page where you find tutorials, webinars, cases of use, among others.

Multiple Independent Sites: Advanced tools for a successful analysis.

AFFINImeter

Isothermal titration Calorimetry experiments of a ligand binding to a macromolecule with multiple independent sites

A successful Isothermal Titration Calorimetry (ITC) experiment requires the acquisition of high quality experimental data together with a careful analysis. Choosing the right binding model to fit the ITC isotherm is critical in order to get the true thermodynamic profile of the interaction. Often, the main limitation to achieve good results arises when the evaluation software lacks of the mathematical model that best describes our binding experiment. A good example is the case of a ligand binding to a macromolecule with multiple independent sites, i.e ligand – DNA interactions (1). Until now the readily available mathematical models to fit such experiments was limited to one or two sets of “n” independent identical sites; frequently, these models offer a poor description of the interaction due to the inherent higher complexity of the system, where many distinct binding equilibria coexist.

 

Multiple Sets of Independent Sites

AFFINImeter ITC offers an unlimited number of user-defined binding models. Particularly, it counts with a feature to easily design models based on multiple independent binding sites. Here, a model with a number of sets of independent sites can be created with no limitation in the number of sets or sites. Noteworthy, the number of sites in each set can be considered as a fitting parameter throughout the data analysis. As an illustration, the following figure shows the reaction parameters of a model generated with AFFINImeter that describes a ligand binding to a receptor having 3 sets of sites, each set having an unknown number of sites. Fitting the experimental data to such model yields the microscopic association constant (K) and the change in enthalpy (ΔH) of the ligand binding to each site type, and the number of sites in each set (n).

Scheme of the interaction of a ligand with a multisite receptor
Reaction parameters table of a model that describes the interaction of a ligand (in syringe) with a multi-site receptor (in cell) having 3 sets of independent sites. Note that the option “Fit” was checked to consider the number of sites (n) as fitting parameters.

These binding models, described by numerous variable parameters, may end up in an over-parameterized fitting function. Thus, the best strategy to achieve a robust and consistent analysis involves the global fitting of several ITC curves acquired under different experimental conditions. In this sense, AFFINImeter also supports global fitting of multiple isotherms wherein parameter linkage between curves is used to decrease the relative number of estimated parameters per experiment.

References:
(1) Methods 2007, 42, 162–172.